

Es gibt viele Gründe(*) dafür, Nachrichten zu verschlüsseln, einer der überzeugendsten ist die Tatsache, dass ein grosser Teil unserer schriftlichen Kommunikation über digitale Medien abgewickelt wird, deren transportierte Inhalte prinzipiell automatisch und flächendeckend mitgelesen und ausgewertet werden können. Aber auch der Schutz der eigenen Privatspäre und die potentielle Unsicherheit bei Transaktionen über das Internet sind Anlässe genug, Nachrichten gegen Einsichtnahme und Veränderung durch Unbefugte zu sichern.
So etwa bei Bestellungen bei Online-Versandhäusern, bei Bankgeschäften, beim Leisten elektronischer Unterschriften.
Die Lehre von den Geheimschriften hat mittlerweile einen Stand erreicht, bei dem jedem Internet-User Kryptographie-Methoden zur Verfügung stehen, manchmal von den Betreibern von Sites verwendet, manchmal auch auf eigene Initiative hin eingesetzt.
Im folgenden werden die Grundbegriffe dieser Wissenschaft von den Geheimschriften erläutert und ein spezielles Verfahren näher beschrieben, PGP, das einen starken und dabei kostenlosen Schutz von Nachrichten erlaubt.
Einige Definitionen:
Klartext(*) nennt man den Text, wie er unverschlüsselt aussieht.
Geheimtext(*) ist der verschlüsselte Text.
Eine Chiffre(*) bezeichnet die Regel, nach der Buchstaben des Klartexts gegen andere Buchstaben vertauscht werden, damit der Geheimtext daraus entsteht.
Der Schlüssel(*) ist eine Zeichenkette, die den Verschlüsselungs- oder Entschlüsselungs-Algorithmus steuert. Jeder, der im Besitz des richtigen Schlüssels ist, kann also aus dem Geheimtext den Klartext erzeugen.
Codebrecher(*) versuchen, Geheimtext zu entschlüsseln, ohne im Besitz des Schlüssels zu sein.
Digitale Signaturen(*) sichern, dass der Text während der Übertragung nicht verändert wurde und vom Besitzer des öffentlichen Schlüssels stammt.
Hash-Funktionen erzeugen einen Auszug aus dem Text, der zum Zweck des Signierens mit dem privaten Schlüssel chiffriert wurde.
Zertifizierung(*) soll sicherstellen, dass ein Schlüssel wirklich zu einer bestimmten Person oder Institution gehört.
Ein Julius Caesar zugeschriebenes Verfahren, Nachrichten geheim zu halten, bestand darin, alle Buchstaben des Textes um die gleiche Anzahl von Buchstaben in der Position im Alphabet zu verschieben. Der Schlüssel ist dann genau diese Zahl, um die die Buchstaben verschoben wurden.
Folgender ist ein Text, der so verschlüsselt wurde:
Kdeh qxq dfk Sklorvrsklh Mxulvwhuhl xqg PhglClq Xqg ohlghu dxfk Wkhrorjlh Gxufkdxv vwxglhuw plw khl hp Ehp kq Gd vwhk lfk qxq lfk duphu Wru Xqg elq vr noxj dov zlh Cxyru Khl h Pdjlvwhu khl h Grnwru jdu Xqg Clhkh vfkrq dq glh Chkhq Mdku Khudxi khude xqg txhu xqg nuxpp Phlqh Vfk ohu dq ghu Qdvh khuxp Xqg vhkh gd zlu qlfkwv zlvvhq n qqhq Gdv zloo plu vfklhu gdv KhuC yhueuhqqhq ]zdu elq lfk jhvfkhlwhu dov doo glh Odiihq Grnwruhq Pdjlvwhu Vfkuhlehu xqg Sidiihq Plfk sodjhq nhlqh Vnuxsho qrfk ]zhliho I ufkwh plfk zhghu yru K ooh qrfk Whxiho Gdi u lvw plu dxfk dooh Iuhxg hqwulvvhq Elogh plu qlfkw hlq zdv Uhfkwv Cx zlvvhq Elogh plu qlfkw hlq lfk n qqwh zdv ohkuhq Glh Phqvfkhq Cx ehvvhuq xqg Cx ehnhkuhq Dxfk kde lfk zhghu Jxw qrfk Jhog Qrfk Hku xqg Khuuolfknhlw ghu Zhow Hv p fkwh nhlq Kxqg vr o qjhu ohehq Guxp kde lfk plfk ghu Pdjlh hujhehq Re plu gxufk Jhlvwhv Nudiw xqg Pxqg Qlfkw pdqfk Jhkhlpqlv z ugh nxqg Gd lfk qlfkw phku plw vdxuhp Vfkzhl ]x vdjhq eudxfkh zdv lfk qlfkw zhl Gd lfk hunhqqh zdv glh Zhow Lp Lqqhuvwhq Cxvdpphqk ow Vfkdx dooh Zlunhqvnudiw xqg Vdphq Xqg wx qlfkw phku lq Zruwhq nudphq
Es ist nun reine Fleißarbeit, alle Möglichkeiten der Verschiebung durchzuprobieren, um so den dann plötzlich erscheinenden Klartext vor sich zu haben. Dieser Aufwand, der letztlich immer genügt, um den Code zu brechen, war in der Antike noch verhältnismäßig groß, heutzutage ist es eine Sache von Millisekunden, mittels brute force, also dem Durchprobieren aller möglicher Schlüssel, aus dem Buchstabensalat lesbaren Text zu erzeugen.
Doch es geht auch raffinierter: denn so chaotisch der Geheimtext auf den ersten Blick auch aussehen mag, so hat er doch auffällige Eigenheiten. Etwa die Verteilung der Buchstaben:
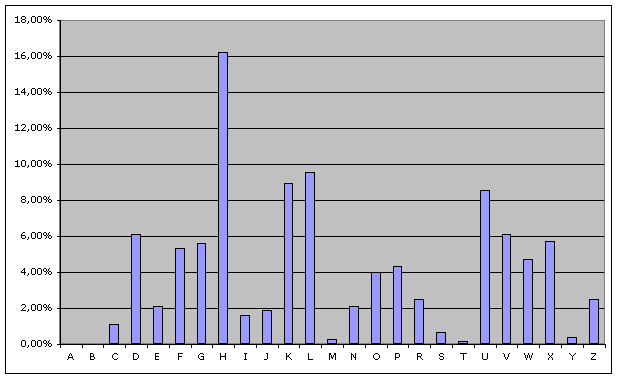
Vergleicht man diese mit der durchschnittlichen der deutschen Sprache, für die sie für die häufigsten Buchstaben lautet:
e: 18,0%
n: 11,1%
r: 8,0%
s: 7,5%,
dann wird schnell klar, dass das "H" ein "E" sein muss, der Schlüssel also den Wert "3" hat.
Probieren Sie einmal herauszubekommen, wie der Klartext lautet!
Caesars Chiffre ist keine starke Kryptographie. Starke Kryptographie hätte Eigenschaften(*), die wir auch an heutezutage unknackbaren Codes schätzen:
Es ist nicht sehr aufwändig, einen Klartext zu verschlüsseln, der umgekehrte Weg, vom Geheimtext zum Klartext, erfordert sehr viel mehr Aufwand. Das mathematische Verfahren, das eine solche Eigenschaft hat, nennt man eine Einweg- oder eine Falltür-Funktion(*). Leicht in die eine, schwer in die andere Richtung.
Ein Beispiel für Falltürfunktionen ist etwa die Multiplikation bzw. die Primfaktorzerlegung:
Sind a und b Primzahlen, dann ist die Aufgabe a*b = x schnell gelöst, aber gegeben x, ist es sehr aufwändig, a und b zu ermitteln, weil es das Durchprobieren sehr vieler Möglichkeiten erfordert.
Z.B.: 967*773=747.491
Die Multiplikation ist schnell gemacht, auch ohne Computer. Aber probieren Sie einmal herauszufinden, welche Faktoren in 747.491 stecken!
Identifizieren Sie den Klartext mit der ersten Zahl, etwa, indem Sie das Bitmuster als Binärzahl verwenden, identifizieren Sie den Schlüssel mit der zweiten, dann haben Sie als Produkt den Geheimtext. Der Geheimtext ist schnell aus Klartext und Schlüssel zu berechnen, aber nur schwer lassen sich Schlüssel und Klartext aus dem Geheimtext berechnen.
Die tatsächlich verwendeten Verfahren funktionieren im Detail noch ein wenig anders, aber im Prinzip nach der hier skizzierten Methode.
Dennoch ist dieser schwierigere Weg, die Kryptoanalyse, das Code-Brechen, nur eine Frage der investierten Arbeit. Was Caesars Code also von den heute praktisch unknackbaren unterscheidet, ist der Aufwand, der zum Knacken erforderlich ist. Das Maß ist in heutigen Zeiten also: wie lange müssen wirklich schnelle Computer rechnen, bis sie den Code gebrochen haben? Die Antwort für wirklich starke Verschlüsselung muss demnach lauten: länger als für den Codebrecher zumutbar, etwa bis zuzm Ende des Universums, bei heutiger Rechnerleistung. Das setzt natürlich voraus, dass niemand eine vielleicht geheime Methode kennt,das Entschlüsselungs-Problem sehr viel einfacher zu lösen. Einen mathematischen Beweis für die Unknackbarkeit der jetzt im Gebrauch befindlichen Methoden gibt es nicht. Es gibt nur Hinweise aus der Konkurrenz der Kryptographen untereinander, deren Leidenschaft es ist, die Methoden der Konkurrenten als überwindbar zu demaskieren, und dafür werden gelegentlich auch Wettbewerbe veranstaltet.
Konventionelle Kryptographie verwendet für die Ver- und die Entschlüsselung denselben Schlüssel:
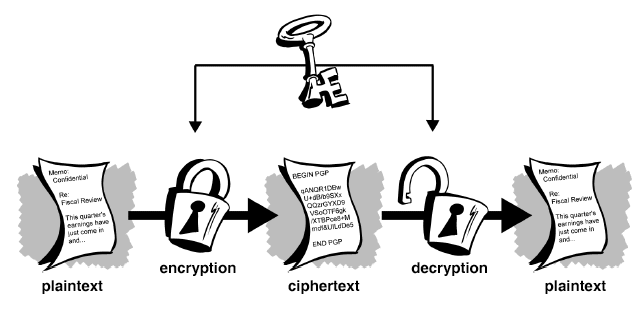
(Graphik aus: An Introduction to Cryptography, PGP Corp., einer lesenswerten Kurzeinführung in die Kryptographie)
Symmetrische Verfahren mit einem Schlüssel sind schnell und, solange der Schlüssel geheim bleibt, auch sicher. Vertreter sind:
DES (Data Encryption Standard): verschlüsselt immer Blocks von jeweils 64 Bit, Schlüssellänge ist 56 Bit, umfasst also 2 hoch 56 = 7 * 10 hoch 16, das sind 70 Millionen Milliarden Kombinationen. Unter Aufbringung von sehr viel Mühe ist der Code durch Ausprobieren (fast) aller Schlüssel knackbar.
Triple DES verwendet DES drei Mal mit zwei verschiedenen Schlüsseln, womit der Schlüssel auf 112 Bits verlängert wurde. Unknackbar nach heutigem Wissen.
AES (Advanced Encryption Standard) von Rijndael und Daemen mit 128 Bit Schlüssellänge und schneller als Triple DES. Unknackbar.
So sicher diese Verfahren sind, so kranken sie an dem Problem, den Schlüssel zwischen Absender und Empfänger austauschen zu müssen. Im Falle der unsicheren Internet-Kommunikation lässt sich der Schlüssel also nicht einfach weitergeben, etwa per Mail: er könnte abgehört und damit unbrauchbar werden.
Deshalb sind Verfahren entwickelt worden, die mit zwei Schlüsseln arbeiten, von denen einer geheim und einer öffentlich sein kann. Mit dem öffentlichen wird verschlüsselt, nur der geheime, private kann entschlüsseln:

Es muss also nur der öffentliche Schlüssel ausgetauscht werden. Das macht aber nichts, mit diesem lässt sich eine verschlüsselte Nachricht ja nicht lesen, das geht nur mit dem privaten, geheim zu haltenden Schlüssel.
Natürlich hängen die beiden Schlüssel voneinander ab: sie müssen gemeinsam von demselben Algorithmus erzeugt werden, einen Teil, den öffentlichen, lässt man alle die wissen, von denen man verschlüsselte Nachrichten bekommen möchte (alle Internet-Nutzer etwa, indem man sie auf einen Server legt), den anderen Teil, mit dem die Entschlüsselung möglich ist, hält man geheim. Nie muss ein geheimer Schlüssel ausgetauscht werden, jeder kann mit jedem verschlüsselte Botschaften tauschen, ohne denjenigen je getroffen zu haben.
Verfahren, die so etwas leisten, heißen Elgamal, RSA, Diffie-Hellman und DSA.
Martin Warnke und Trebitsch Lincoln wollen E-Mails miteinander austauschen, die niemand anderer lesen kann. Dazu erzeugen beide mit demselben Verfahren ihr Schlüsselpaar, bestehend aus dem privaten und dem öffentlichen Schlüssel. Ihre öffentlichen Schlüssel publizieren sie auf einem Schlüssel-Server oder schicken sie im Klartext per Mail an den anderen.
MWs öffentlicher Schlüssel zB lautet (mit PGP erzeugt, s.u.):
-----BEGIN PGP PUBLIC KEY BLOCK-----
Version: PGP 8.0
mQGiBD30waARBADiUyPvnHxJ8pWgAPE9H8oyPDFuBv617463kuCSCcGLFnwLek2A
lpwkU1SIs39lRSCkBB6bJseMYnMDLG0K04hDqDiFh/Ai+iWlAWivH5xMuIuA/l+l
gfUcvDB15YwRdpOMnEJ1UACvrC8VRh5ZKoqQM5K+TlIRFcANRVZUUOlmywCg/2fx
9vGtwg6Uj2CcR2HQlpkrLOsD/Ri1niElJTl3iQCvGdNp40UiTCpTjBA3Ulp60jy7
tkoAlO/bOPkFpTaTh+Q7C5WXfy2KPhAoX7qrg9/+XGSruy591CSOsGEOMN82+EL6
KoS6im0IFXTxSak7mTIdKOG1ykV4BgZgTPOgKJ17iWmuQvcTzh/XUO71rkHRYIg/
246bA/42OidqP8uwxX/arypTMi2uQMjY4CgVIKRac1A8fEuCQxjPtR5+SQTuQWzx
fKA3++ZzgcmMkWSAg7Mq+iwA4ovBxlaqrwupmVlDTQ0eUoUXzgTwdNXCuZAL7pWY
zC0Pj0IS9EBKstZtWB3i+zxbpL6CCYN/UH0AAvOHd/9UzC1IdbQrRHIuIE1hcnRp
biBXYXJua2UgPHdhcm5rZUB1bmktbHVlbmVidXJnLmRlPokAWAQQEQIAGAUCPfTB
oAgLCQgHAwIBCgIZAQUbAwAAAAAKCRDt9VsHGWvNdFMSAKD3wc0v1DlbJR3NMe+Y
km3furKF4gCeJIX/TlfoAA99vt0ODDMJlCG+wRi5Ag0EPfTBoRAIAPZCV7cIfwgX
cqK61qlC8wXo+VMROU+28W65Szgg2gGnVqMU6Y9AVfPQB8bLQ6mUrfdMZIZJ+AyD
vWXpF9Sh01D49Vlf3HZSTz09jdvOmeFXklnN/biudE/F/Ha8g8VHMGHOfMlm/xX5
u/2RXscBqtNbno2gpXI61Brwv0YAWCvl9Ij9WE5J280gtJ3kkQc2azNsOA1FHQ98
iLMcfFstjvbzySPAQ/ClWxiNjrtVjLhdONM0/XwXV0OjHRhs3jMhLLUq/zzhsSlA
GBGNfISnCnLWhsQDGcgHKXrKlQzZlp+r0ApQmwJG0wg9ZqRdQZ+cfL2JSyIZJrqr
ol7DVekyCzsAAgIH/R8M0mYSRsG2vp1xH9LM/f6D/qXjhXuE4w2NJrxlVKobPa9k
Z5bRkCvVkFrsB8yCWe3DfdsBIPq2ezIRZ5L72r+8LI9xsRuCAK70WPVUc6zhsP28
lFMTgMhaMHpfUgUXwRtPcwl/WkuSeHniQuOK+nK70+VjptkT4VDiv5bqLf+a4erA
Be5qyA1kn5E/FoaKFF1e6qoZ4FvTdZIwGxGcbx9v6x4JLattNDbLH/I22fvm3X4X
h4KJz6Girhpwyoulm+xn3XfzlHjrdWJCLKqIaBClP9D+em7KG37CFluWFgmUX1Zv
YcaSImnuYawBwr41yXCnIRtcz2wzwOE2HFvcQ+GJAEwEGBECAAwFAj30waEFGwwA
AAAACgkQ7fVbBxlrzXQKuACg3besUGu5PTSzyZp5YoIlO/eyGGUAoPnA89QHoo0f
YpW5KpSjAnpH6F1/
=4ZLp
-----END PGP PUBLIC KEY BLOCK-----
MW besitzt dann: MW-p und MW-ö, seine beiden eigenen Schlüssel, und TL-ö, den öffentlichen von Trebitsch Lincoln, vielleicht noch sehr viele weitere öffentliche Schlüssel.
TL besitzt: TL-p, TL-ö und MW-ö und viele andere öffentliche Schlüssel.
MW verschlüsselt dann mit TL-ö seine Nachricht und sendet sie verschlüsselt über das unsichere Internet.
TL empfängt sie und kann sie erst dann lesen, wenn er mit seinem privaten Schlüssel TL-p die Nachricht entschlüsselt.
PGP ist das Akronym für "Pretty Good Privacy", "ziemlich guter Datenschutz". PGP realisiert ein starkes asymmetrisches Verfahren. Es ist im Kern public domain, also für alle kostenlos und lizenzfrei zu haben, es gibt auch komfortable Oberflächen für eine bequeme Integration von PGP in die elektronische Post, für das Verschlüsseln von Dateien, den Austausch von öffenlichen Schlüsseln und, nicht zuletzt, die Erzeugung des Einmal-Schlüssels (s.u.).
PGP wurde von Phil Zimmerman entwickelt und funktioniert als hybrides Verfahren, das mit symmetrischen und asymmetrischen Techniken operiert. Die tatsächliche Verschlüsselung des Klartextes wird mit einer schnell arbeitenden konventionellen symmetrischen Chiffre bewerkstelligt, der Schlüssel selbst, gültig nur für die eine Übertragung, wird mit einem öffentlichen Schlüssel ver- und mit dem privaten entschlüsselt:
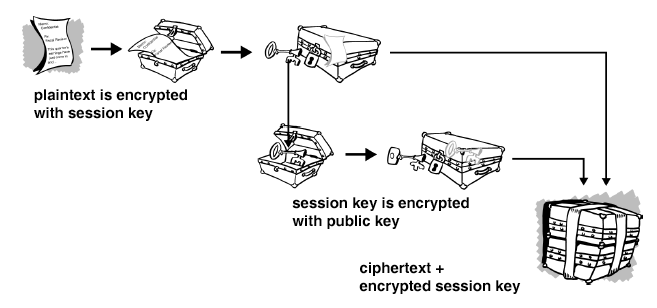
Weil der Klartext im Allgemeinen sehr viel länger als der Schlüssel ist, lohnt diese Mischung aus symmetrischen und asymmetrischen Verfahren in der Summe.
Auf der Empfängerseite entschlüsselt man den mitgeschickten Einmal-Schlüssel mit seinem privaten, danach entschlüsselt man den Geheimtext mit dem gerade entschlüsselten Einmal-Schlüssel:
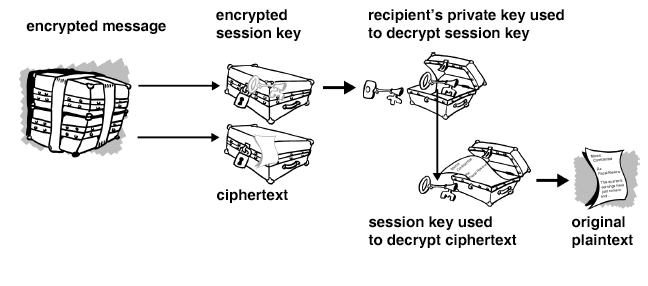
PGP-Progrqamme erledigen die ganze Verwaltung, erzeugen den Einmal-Schlüssel, ver- und entschlüsseln mit den asymmetrischen Paaren. Auszutauschen sind lediglich die öffentlichen Schlüssel und die Geheimtexte.
Codebrechen bei asymmetrischen Verfahren bedeutet, aus dem öffentlichen den privaten Schlüssel zu berechnen, die ja miteinander zusammenhängen müssen. Damit das schwierig genug, also praktisch unmöglich ist, sind die Schlüssel(*) länger als bei symmetrischen Verfahren, 1012 oder 2024 Bits lang.
Zur Sicherheit von Schlüsseln sei die PGP-Corporation zitiert:
"Today, in late 2002, we believe that 128-bit keys will be safe indefinitely, at least until someone invents a usable quantum computer. We also believe that 256-bit keys will be safe indefinitely, even if someone invents a quantum computer. This is why the AES includes options for 128 and 256-bit keys. But history tells is that it’s quite possible someone will think this statement amusingly quaint in a few decades." (aus: An Introduction to Cryptography, S. 15)
Ok, wir können nun Texte so übertragen, dass nur der Empfänger sie lesen kann. Woher weiß dieser aber, wer wirklich der Absender ist? Jede und jeder kann doch, sagen wir, Trebitsch Lincolns öffentlichen Schlüssel nehmen und ihm in, sagen wir, Martin Warnkes Namen eine Mail senden!
Digitale Signaturen, etwa im Rahmen von PGP, lösen dieses Problem. Mit dem privaten Schlüssel des Absenders lassen sich Texte nun auch unterschreiben. Mit Hilfe seines öffentlichen Schlüssels kann dann der Empfänger ermitteln, ob der Absender im Besitz des privaten Schlüssels war, der zum öffentlichen Schlüssel gehört:
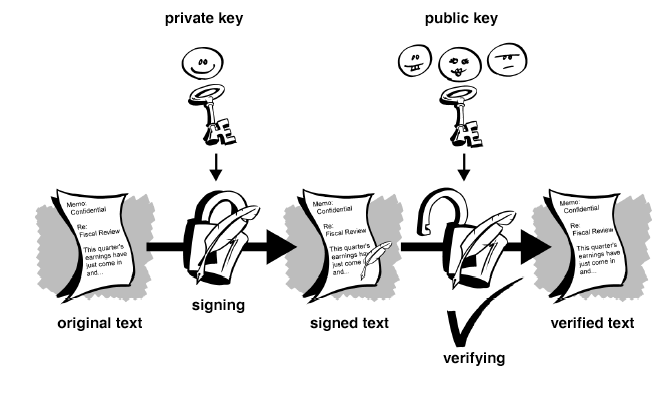
So sieht z.B. eine Mail von MW aus, die er signiert hat:
Von: Martin Warnke <warnke@uni-lueneburg.de>
Datum: Sa, 14. Dez 2002 23:42:30 Europe/Berlin
An: Martin Warnke <warnke@uni-lueneburg.de>
Betreff:
-----BEGIN PGP SIGNED MESSAGE-----
Hash: SHA1
War ich das wirklich selbst?
M
-----BEGIN PGP SIGNATURE-----
Version: PGP 8.0
iQA/AwUBPfuz3e31WwcZa810EQJr7wCgruecIQ7HkAixfkBTn5Kpu9Fmw5MAn0yA
Nz8cTdBVfP128fSWVu8Bnbda
=YwcQ
-----END PGP SIGNATURE-----
Die Signatur stellt sicher, dass es sich um den behaupteten Absender handelt, und dass der Text auf dem Wege nicht verändert wurde, denn die Signatur ändert sich mit dem übertragenen Text auf eine Weise, dass schon minimale Änderungen am Text zu einer völlig anderen Unterschrift führen.
Seine PGP-Applikation kann nun herausfinden, ob diese Mail wirklich vom behaupteten Absender stammt und unverändert geblieben ist:
*** PGP SIGNATURE VERIFICATION ***
*** Status: Good Signature
*** Signer: Dr. Martin Warnke <warnke@uni-lueneburg.de> (0x196BCD74)
*** Signed: 12/14/2002 11:42:37 PM
*** Verified: 12/14/2002 11:45:44 PM
*** BEGIN PGP VERIFIED MESSAGE ***
War ich das wirklich selbst?
M
*** END PGP VERIFIED MESSAGE ***
Die Signatur ist eine mit dem privaten Schlüssel chiffrierte Zusammenfassung, die von einer so genannten Hash-Funktion erzeugt wurde (hash (engl.): Mischmasch, Haschee).
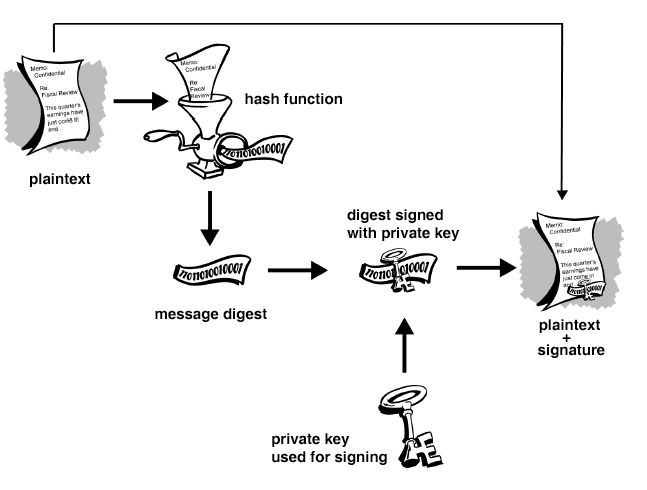
Woher kann man wissen, dass es wirklich die Person ist, die mit ihrem Namen und E-Mail-Adresse hinter einem PGP-Schlüssel-Paar steckt?
Überhaupt nicht, es sei denn, jemand kann das glaubhaft versichern. Solche glaubhaften Versicherungen kommen von CAs: Certificate Authorities. Das sind Institutionen, deren Reputation so gut ist, dass man Echtheits-Zertifikaten Glauben schenkt. Beispiele sind etwa der DFN-Verein, der Heise-Verlag und viele Banken, die dadurch einen sicheren Informationsaustausch mit ihren Kunden ermöglichen.
Will man von einer CA ein Zertifikat, muss man dort vorstellig werden, sich ausweisen oder ein Schreiben der Institution vorlegen, die sich zertifizieren lassen will, oder sonstwie unmittelbar bekannt sein.
Die Zertifikate der CAs sind Signaturen der Schlüssel der Person oder Institution, die sich zertifizieren lassen will. Man kann sie auf dem Schlüssel-Server anschauen und dann entscheiden, ob man den so zertifizierten Schlüssel für echt hält.
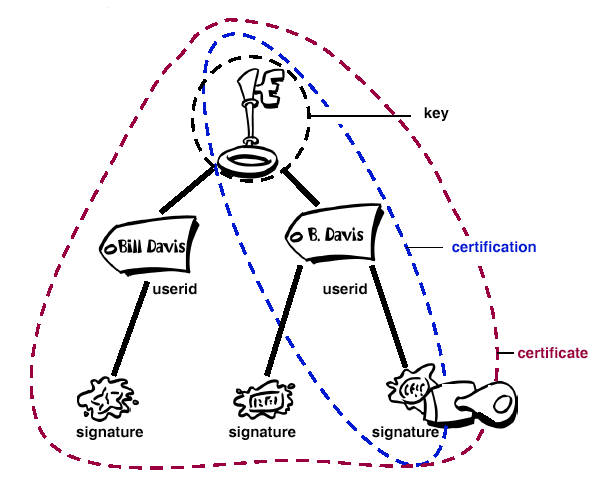
In PGP kann man auch selbst festlegen und veröffentlichen, ob und in wie weit man einer behaupteten Identität traut.
Linksammlung zur Krypto-Debatte
International Association fpr Cryptography Research
The international pgp home site
Electronic Privacy Information Center
Electronic Frontier Foundation
Gesellschaft für Informatik, Fachbereich "Informatik und Gesellschaft"
(*) meint: das ist ein wichtiges Thema.